How To Find The Discriminant Of An Equation

Learning Objectives

• Define the discriminant and apply it to allocate solutions to quadratic equations

The Discriminant

The quadratic formula not only generates the solutions to a quadratic equation, it tells the states about the nature of the solutions. When we consider the discriminant, or the expression under the radical, [latex]{b}^{2}-4ac[/latex], information technology tells us whether the solutions are real numbers or circuitous numbers, and how many solutions of each type to expect. The table below relates the value of the discriminant to the solutions of a quadratic equation.

Value of Discriminant	Results
[latex]{b}^{two}-4ac=0[/latex]	One repeated rational solution
[latex]{b}^{2}-4ac>0[/latex], perfect square	Ii rational solutions
[latex]{b}^{2}-4ac>0[/latex], not a perfect square	Two irrational solutions
[latex]{b}^{two}-4ac<0[/latex]	Ii complex solutions

A General Note: The Discriminant

For [latex]a{x}^{2}+bx+c=0[/latex], where [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] are real numbers, the discriminant is the expression under the radical in the quadratic formula: [latex]{b}^{2}-4ac[/latex]. It tells us whether the solutions are real numbers or complex numbers and how many solutions of each type to await.

Instance

Use the discriminant to find the nature of the solutions to the following quadratic equations:

1. [latex]{x}^{2}+4x+4=0[/latex]
2. [latex]eight{x}^{2}+14x+three=0[/latex]
3. [latex]3{ten}^{ii}-5x - ii=0[/latex]
4. [latex]3{x}^{2}-10x+fifteen=0[/latex]

Nosotros have seen that a quadratic equation may have two real solutions, one real solution, or 2 complex solutions.

In the Quadratic Formula, the expression underneath the radical symbol determines the number and type of solutions the formula will reveal. This expression, [latex]b^{2}-4ac[/latex], is called the discriminant of the equation [latex]ax^{2}+bx+c=0[/latex].

Let's think about how the discriminant affects the evaluation of [latex] \sqrt{{{b}^{ii}}-4ac}[/latex], and how it helps to determine the solution fix.

• If [latex]b^{2}-4ac>0[/latex], then the number underneath the radical will be a positive value. Yous can always find the square root of a positive, so evaluating the Quadratic Formula will result in two real solutions (one past adding the positive square root, and one by subtracting it).
• If [latex]b^{2}-4ac=0[/latex], then you will be taking the foursquare root of [latex]0[/latex], which is [latex]0[/latex]. Since adding and subtracting [latex]0[/latex] both requite the same result, the "[latex]\pm[/latex]" portion of the formula doesn't matter. At that place will be one real repeated solution.
• If [latex]b^{2}-4ac<0[/latex], so the number underneath the radical will be a negative value. Since you cannot find the square root of a negative number using real numbers, there are no existent solutions. However, you can use imaginary numbers. You volition then have two complex solutions, one by adding the imaginary foursquare root and one past subtracting it.

Example

Use the discriminant to determine how many and what kind of solutions the quadratic equation [latex]x^{2}-4x+10=0[/latex] has.

In the last example, we volition depict a correlation between the number and type of solutions to a quadratic equation and the graph of it's corresponding part.

Example

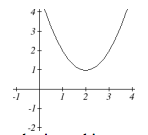
Use the following graphs of quadratic functions to determine how many and what type of solutions the corresponding quadratic equation [latex]f(ten)=0[/latex] will have.  Determine whether the discriminant will be greater than, less than, or equal to zero for each.

a.

b.

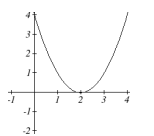
c.

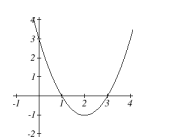
We tin can summarize our results every bit follows:

Discriminant	Number and Type of Solutions	Graph of Quadratic Function
[latex]b^{ii}-4ac<0[/latex]	two complex solutions	will not cross the x-axis
[latex]b^{2}-4ac=0[/latex]	one real repeated solution	will touch x-axis once
[latex]b^{2}-4ac>0[/latex]	ii real solutions	will cantankerous x-axis twice

In the following video we show more than examples of how to use the discriminant to describe the blazon of solutions to a quadratic equation.

Summary

The discriminant of the Quadratic Formula is the quantity under the radical, [latex] {{b}^{two}}-4ac[/latex]. It determines the number and the type of solutions that a quadratic equation has. If the discriminant is positive, there are [latex]2[/latex] real solutions. If it is [latex]0[/latex], there is [latex]ane[/latex] real repeated solution. If the discriminant is negative, in that location are [latex]2[/latex] circuitous solutions (but no existent solutions).

The discriminant can likewise tell us about the behavior of the graph of a quadratic office.

Source: https://courses.lumenlearning.com/waymakerintermediatealgebra/chapter/read-the-discriminant/

Posted by: devinemarisch.blogspot.com

Share this post